I know it’s a weird way to start a blog with a negative, but there was a wave of discussion in the last few days that I think serves as a good hook for some topics on which I’ve been thinking recently. It all started with a post in the Simply Stats blog by Jeff Leek on the caveats of using deep learning in the small sample size regime. In sum, he argues that when the sample size is small (which happens a lot in the bio domain), linear models with few parameters perform better than deep nets even with a modicum of layers and hidden units. He goes on to show that a very simple linear predictor, with top ten most informative features, performs better than a simple deep net when trying to classify zeros and ones in the MNIST dataset using only 80 or so samples. This prompted Andrew beam to write a rebuttal in which a properly trained deep net was able to beat the simple linear model, even with very few training samples. This back-and-forth comes at a time where more and more researchers in biomedical informatics are adopting deep learning for various problems. Is the hype real or are linear models really all we need? The answer, as alwyas, is that it depends. In this post, I want to visit use cases in machine learning where using deep learning does not really make sense as well as tackle preconceptions that I think prevent deep learning to be used effectively, especially for newcomers.

Breaking deep learning preconceptions

First, let’s tackle some preconceptions that I perceive most folks outside the field have that turn out to be half-truths. There’s two broad ones and one a bit more technical that I’m going to elaborate on. This is somewhat of an extension to Andrew Beam’s excellent “Misconceptions” section in his post.

Deep learning can really work on small sample sizes

Deep learning’s claim to fame was in a context with lots of data (remember that the first Google brain project was feeding lots of youtube videos to a deep net), and ever since it has constantly been publicized as complex algorithms running in lots of data. Unfortunately, this big data/deep learning pair somehow translated into the converse as well: the myth that it cannot be used in the small sample regime. If you have just a few samples, tapping into a neural net with a high parameter-per-sample ratio may superficially seem like a sure road to overfitting. However, just considering sample size and dimensionality for a given problem, be it supervised or unsupervised, is sort of modeling the data in a vacuum, without any context. It is probably the case that you have data sources that are related to your problem, or that there’s a strong prior that a domain expert can provide, or that the data is structured in a very particular way (e.g. is encoded in a graph or image). In all of these cases, there’s a chance deep learning can make sense as a method of choice – for example, you can encode useful representations of bigger, related datasets and use those representations in your problem. A classic illustration of this is common in natural language processing, where you can learn word embeddings on a large corpus like Wikipedia and then use those as embeddings in a smaller, narrower corpus for a supervised task. In the extreme, you can have a set of neural nets jointly learn a representation and an effective way to reuse the representation in small sets of samples. This is called one-shot learning and has been successfully applied in a number of fields with high-dimensional data including computer vision and drug discovery.

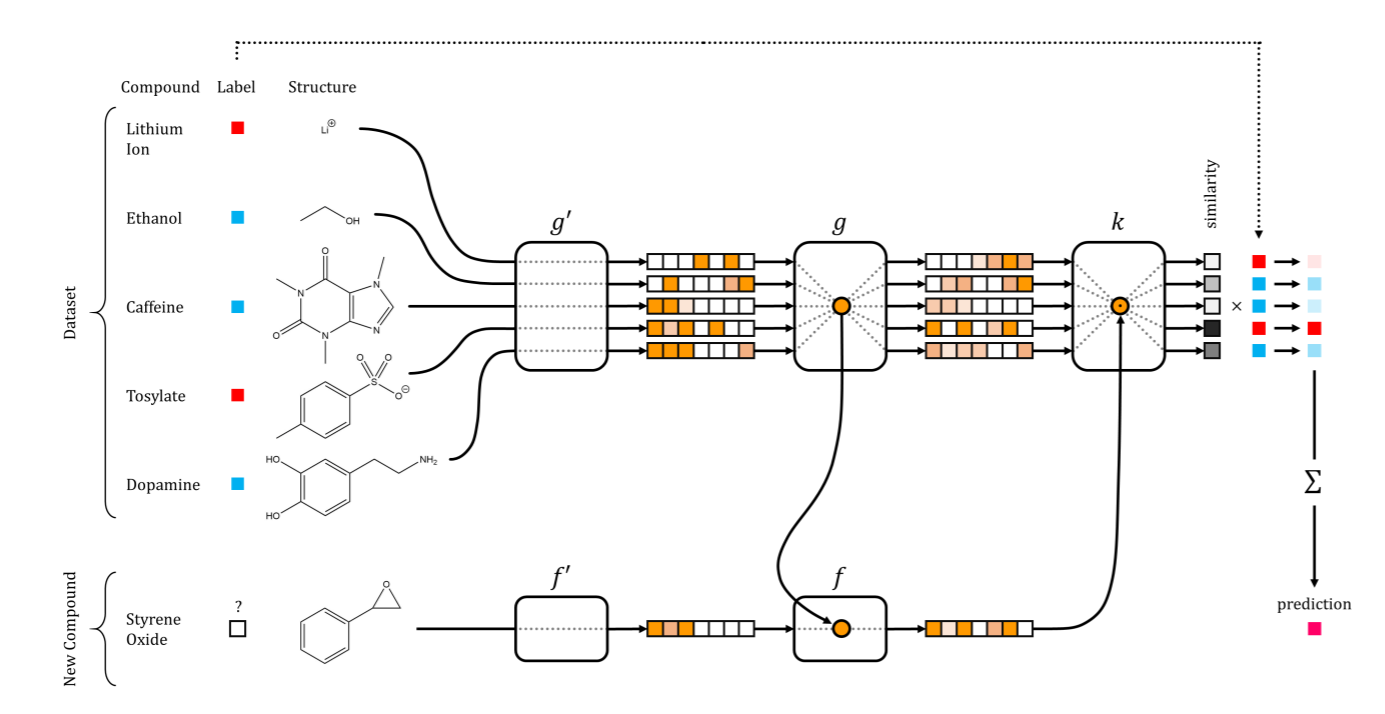One-shot learning networks for drug discovery, taken from Altae-Tran et al. ACS Cent. Sci. 2017

Deep learning is not the answer to everything

The second preconception I hear the most is the hype. Many yet-to-be practitioners expect deep nets to give them a mythical performance boost just because it worked in other fields. Others are inspired by impressive work in modeling and manipulating images, music, and language – three data types close to any human heart – and rush headfirst into the field by trying to train the latest GAN architecture. The hype is real in many ways. Deep learning has become an undeniable force in machine learning and an important tool in the arsenal of any data modeler. It’s popularity has brought forth essential frameworks such as tensorflow and pytorch that are incredibly useful even outside deep learning. It’s underdog to superstar origin story has inspired researchers to revisit other previously obscure methods like evolutionary strategies and reinforcement learning. But it’s not a panacea by any means. Aside from no-free-lunch considerations, deep learning models can be very nuanced and require careful and sometimes very expensive hyperparameter searches, tuning, and testing (much more on this later in the post). Besides, there are many cases where using deep learning just doesn’t make sense from a practical perspective and simpler models work much better.

Deep learning is more than .fit()

There is also an aspect of deep learning models that I see gets sort of lost in translation when coming from other fields of machine learning. Most tutorials and introductory material to deep learning describe these models as composed by hierarchically-connected layers of nodes where the first layer is the input and the last layer is the output and that you can train them using some form of stochastic gradient descent. After maybe some brief mentions on how stochastic gradient descent works and what backpropagation is, the bulk of the explanation focuses on the rich landscape of neural network types (convolutional, recurrent, etc.). The optimization methods themselves receive little additional attention, which is unfortunate since it’s likely that a big (if not the biggest) part of why deep learning works is because of those particular methods (check out, e.g. this post from Ferenc Huszár’s and this paper taken from that post), and knowing how to optimize their parameters and how to partition data to use them effectively is crucial to get good convergence in a reasonable amount of time. Exactly why stochastic gradients matter so much is still unknown, but some clues are emerging here and there. One of my favorites is the interpretation of the methods as part of performing Bayesian inference. In essence, every time that you do some form of numerical optimization, you’re performing some Bayesian inference with particular assumptions and priors. Indeed, there’s a whole field, called probabilistic numerics, that has emerged from taking this view. Stochastic gradient descent is no different, and recent work suggests that the procedure is really a Markov chain that, under certain assumptions, has a stationary distribution that can be seen as a sort of variational approximation to the posterior. So when you stop your SGD and take the final parameters, you’re basically sampling from this approximate distribution. I found this idea to be illuminating, because the optimizer’s parameters (in this case, the learning rate) make so much more sense that way. As an example, as you increase the learning parameter of SGD the Markov chain becomes unstable until it finds wide local minima that samples a large area; that is, you increase the variance of procedure. On the other hand, if you decrease the learning parameter, the Markov chain slowly approximates narrower minima until it converges in a tight region; that is, you increase the bias for a certain region. Another parameter, the batch size in SGD, also controls what type of region the algorithm converges two: wider regions for small batches and sharper regions with larger batches.

SGD prefers wide or sharp minima depending on its learning rate or batch size

This complexity means that optimizers of deep nets become first class citizens: they are a very central part of the model, every bit as important as the layer architecture. This doesn’t quite happen with many other models in machine learning. Linear models (even regularized ones, like the LASSO) and SVMs are convex optimization problems for which there is not as much nuance and really only one answer. That’s why folks that come from other fields and/or using tools like scikit-learn are puzzled when they don’t find a very simple API with a .fit() method (although there are some tools, like skflow, that attempt to bottle simple nets into a .fit() signature, I think it’s a bit misguided since the whole point of deep learning is its flexibility).

When not to use deep learning

So, when is deep learning not ideal for a task? From my perspective, these are the main scenarios where deep learning is more of a hinderance than a boon.

Low-budget or low-commitment problems

Deep nets are very flexible models, with a multitude of architecture and node types, optimizers, and regularization strategies. Depending on the application, your model might have convolutional layers (how wide? with what pooling operation?) or recurrent structure (with or without gating?); it might be really deep (hourglass, siamese, or other of the many architectures?) or with just a few hidden layers (with how many units?); it might use rectifying linear units or other activation functions; it might or might not have dropout (in what layers? with what fraction?) and the weights should probably be regularized (l1, l2, or something weirder?). This is only a partial list, there are lots of other types of nodes, connections, and even loss functions out there to try. Those are a lot of hyperparameters to tweak and architectures to explore while even training one instance of large networks can be very time consuming. Google recently boasted that its AutoML pipeline can automatically find the best architecture, which is very impressive, but still requires more than 800 GPUs churning full time for weeks, something out of reach for almost anyone else. The point is that training deep nets carries a big cost, in both computational and debugging time. Such expense doesn’t make sense for lots of day-to-day prediction problems and the ROI of tweaking a deep net to them, even when tweaking small networks, might be too low. Even when there’s plenty of budget and commitment, there’s no reason not to try alternative methods first even as a baseline. You might be pleasantly surprised that a linear SVM is really all you needed.

Interpreting and communicating model parameters/feature importances to a general audience

Deep nets are also notorious for being black boxes with high predictive power but low interpretability. Even though there’s been a lot of recent tools like saliency maps and activation differences that work great for some domains, they don’t transfer completely to all applications. Mainly, these tools work well when you want to make sure that the network is not deceiving you by memorizing the dataset or focusing on particular features that are spurious, but it is still difficult to interpret per-feature importances to the overall decision of the deep net. In this realm, nothing really beats linear models since the learned coefficients have a direct relationship to the response. This is especially crucial when communicating these interpretations to general audiences that need to make decisions based on them. Physicians for example need to incorporate all sorts of disparate data to elicit a diagnosis. The simpler and more direct relationship between a variable and an outcome, the better a physician will leverage it and not under/over-estimate it’s value. Further, there are cases where the accuracy of the model (typically where deep learning excels at) is not as important as interpretability. For example, a policy maker might want to know the effect some demographic variable has on e.g. mortality, and will likely be more interested in a direct approximation of this relationship than in the accuracy of the prediction. In both of these cases, deep learning is at a disadvantage compared to simpler, more penetrable methods.

Establishing causal mechanisms

The extreme case of model interpretability is when we are trying to establish a mechanistic model, that is, a model that actually captures the phenomena behind the data. Good examples include trying to guess whether two molecules (e.g. drugs, proteins, nucleic acids, etc.) interact in a particular cellular environment or hypothesizing if a particular marketing strategy is having an actual effect on sales. Nothing really beats old-style Bayesian methods informed by expert opinion in this realm; they are our best (if imperfect) way we have to represent and infer causality. Vicarious has some nice recent work illustrating why this more principled approach generalizes better than deep learning in videogame tasks.

Learning from “unstructured” features

This one might be up for debate. I find that one area in which deep learning excels at is finding useful representations of the data for a particular task. A very good illustration of this is the aforementioned word embeddings. Natural language has a rich and complex structure that can be approximated with “context-aware” networks: each word can be represented in a vector that encodes the context in which it is mostly used. Using word embeddings learned in large corpora for NLP tasks can sometimes provide a boost in a particular task on another corpus. However, it might not be of any use if the corpus in question is completely unstructured. For example, say you are trying to classify objects by looking at unstructured lists of keywords. Since the keywords are not used in any particular structure (like in a sentence), it’s unlikely that word embeddings will help all that much. In this case, the data is truly a bag of words and such representations are likely sufficient for the task. A counter-argument to this might be that word embeddings are not really that expensive if you use pretrained ones and may capture keyword similarity better. However, I still would prefer to start with the bag of words representation and see if I can get good predictions. After all, each dimension of the bag of words is easier to interpret than the corresponding word embedding slot.

The future is deep

The deep learning field is hot, well-funded, and moves crazy fast. By the time you read a paper published in a conference, it’s likley there are two or three iterations on it that already deprecate it. This brings a big caveat to the points I’ve made above: deep learning might still be super useful for these scenarios in the near future. Tools for interpretation of deep learning models for images and discrete sequences are getting better. Recent software such as Edward marry Bayesian modeling and deep net frameworks, allowing for quantification of uncertainty of neural network parameters and easy Bayesian inference via probabilistic programming and automated variational inference. In the longer term, there might be a reduced modeling vocabulary that nails the salient properties that a deep net can have and thus reduce the parameter space of stuff that needs to be tried. So keep refreshing your arXiv feed, this post might be deprecated in a month or two.

Edward marries probabilistic programming with tensorflow, allowing for models that are both deep and Bayesian. Taken from Tran et al. ICLR 2017

Back to posts