
Why the machine metaphor has failed in biology and software and the concepts that are replacing it
Much progress has been made in laboratory and computational techniques to probe on populations of cells, molecules, neurons, and training of machine learning models. Thanks to these advances, detailed data of both the dynamics and causal relationships in complex systems is beginning to be commonplace. I believe that the conceptual frameworks used to tackle these data are beginning to converge in several fronts. Processes, flows, and causal uncertainty are the underlying principles emerging from these frameworks and, importantly, they stand at odds with one of the main tools of thought that we have used for centuries now: the machine metaphor. From black holes as computers to cells as biochemical circuitry to brains as cell networks, machine metaphors have been used to describe and dissect basically everything. It is a tantalizing idea: since our design principles of machine modularity, specialization, and composability are powerful, easily parsed, and understood, why shouldn’t everything work this way? Why wouldn’t we be able to understand and engineer basically anything by reducing it to its functional parts? The fields of complexity and systems biology sprung in part from this premise, and there has been [lots] [of] [work] criticizing the machine metaphor – but until now I don’t think we had any certainty of or convergence into what should replace the machine metaphor. In a very abstract way, I’ll attempt to give a glimpse of the frameworks that are rising to replace the machine metaphor, and will try to highlight where they might lead to.
What are machine metaphors?
Machine, mechanistic, computation. These words are associated with precision, speed, and a full understanding of a system to the point that it can be predictably modified and improved. Machine metaphors are in essence reductionist ways to think about how to build or systematically disassemble systems.
There are four main characteristics that machine metaphors share: Modularity: The system is divided into a set of discrete and easily identifiable parts or modules. (De)Composability: The system is a sum of its parts. We can piece together modules to build another system – modularity is not lost when we do so. Purposefulness: A machine is made with a purpose, and is put together to perform a specific task. Further, each part of the machine also has a function that contributes to the overall purpose of the machine. Causal Transparency: If we have a diagram of the machine, we can know what will happen when we remove/add/modify a part of it.
I will highlight how these characteristics break in several ways in two areas that I’m familiar with the most: biology and software.
The machine metaphor in biology
Biological systems have long been idealized as complex machinery: from the mechanics of movement of the human body to the way chemical reactions self organize to give rise to cells and multicellular behavior. “DNA is the software, phenotype the hardware”, “The brain is equivalent to a trillion transistor circuit”, etc. In a way, these metaphors underestimate the challenges faced when studying biological systems, as they suggest a static picture of a system for which we only need to find the blueprint behind them to understand, fix, and tune them. Such conceptualizations are at odds with the forces that actually drive biological systems: evolution at the mid and macro scale and thermal fluctuations at the micro scale. Evolution, for example, depends on selection pressure forces that are constantly at work, varying in intensity and directionality depending on the environment; therefore shaping dynamically molecules, cells, individuals, and populations. Purposefulness of each entity can be gained or lost. This happens when switches in evolutionary pressures guide a region of a genome to acquire a temporary function, giving a fitness boost . After the pressure is gone, this function may vanish in neutral mutation; or the region might be duplicated and branched into a new function entirely. Modularity is not intrinsic to evolving systems but rather emerges.
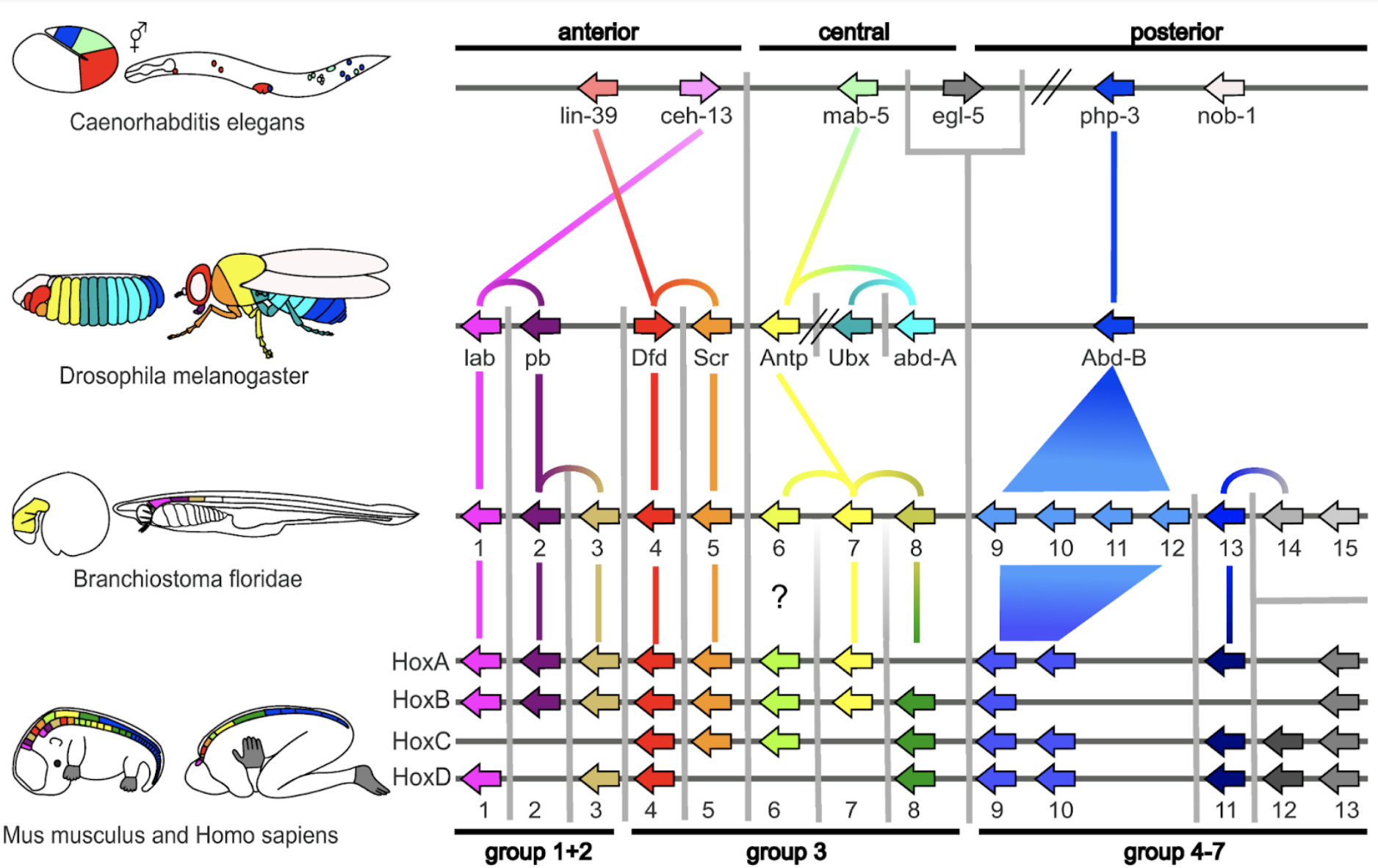 Hox genes are swapped, duplicated and rearranged modularly throughout evolution, changing morphological developmental patterns. From Hueber et al
Hox genes are swapped, duplicated and rearranged modularly throughout evolution, changing morphological developmental patterns. From Hueber et al
In the molecular scale, any concept or quantity only makes sense in averages as the thermal fluctuations that permeate molecular movement become a dominant force. At this scale, causal relationships become a bit blurry and invalidate simple pictures of molecular motors chugging along exactly like their macroscale counterparts. Further complicating the matter, energy sources nudge most of the biological entities, at the molecular and cellular scale, out of equilibrium regimes, regimes in which most of our analytical tools for dissecting machines are known to work. Decomposability of these systems is only partial: take for example the many genes that seem to be associated with the majority of complex traits. This is just a glance of places in biology where the machine metaphor breaks, but I will go into more detail on a couple of examples that, to my knowledge, violate the metaphor’s principles most egregiously.
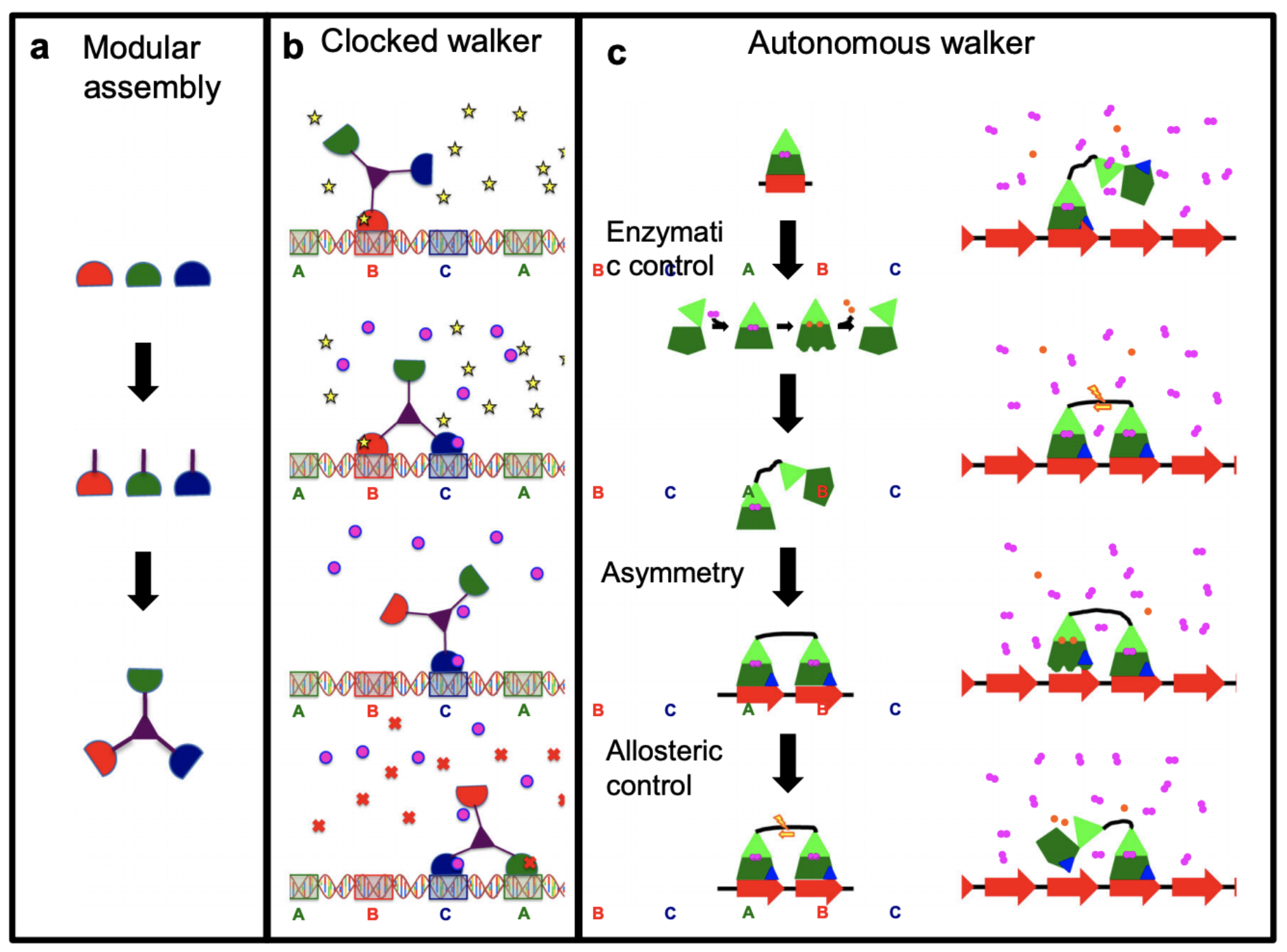 To design molecular motors that “walk” in a DNA track you need to take into account diffusion of reactants that make the molecule “stick or release” as well as diffusion and fluctuations of the motor itself. The whole system is dominated by thermal fluctuations and only makes sense in averages. From Linke et al.
To design molecular motors that “walk” in a DNA track you need to take into account diffusion of reactants that make the molecule “stick or release” as well as diffusion and fluctuations of the motor itself. The whole system is dominated by thermal fluctuations and only makes sense in averages. From Linke et al.
Emergence and divergence of modularity: gene enhancer networks and development
Genes are pieces of the genome that get expressed and translated into a specific protein that are used for one or more tasks in the cell. But what they produce is as important as when they produce it. Part of the elements that regulate when genes are turned on are other pieces of DNA called enhancers. Enhancers are regions of the genome that recruit other proteins called transcriptions factors that activate a nearby gene. Each enhancer has its own necessary condition for activation requiring one or many transcription factors, with various levels of sufficiency (e.g. requiring factors to be oriented in specific ways, etc.) that encode the context where the gene should be activated (e.g. in a given cell type). Of course, transcription factors come from genes themselves and so a network of activations is formed: cascades of genes that turn on and off to coordinate what the cell should do and when. This network is crucial for processes like multicellular development, where various enhancers can dictate when key genes are activated to start and stop forming different parts of the organism. Further, genomic rearrangements such as translocations of enhancers may swap and/or duplicate their activating power elsewhere, perhaps near other genes, effectively rewiring the network – a powerful evolutionary force that achieves large phenotypic changes with relatively little change. At first glance, enhancers might seem a perfect example of modularity: they can really seem like self-contained circuit “gates” that are swapped around by evolution to explore the phenotypic space. However, the conditions by which enhancers are activated are themselves subject to evolution, with each different mechanism of activation subject to different susceptibility to different types of mutation. Consequently, this manifests in different genome sequence conservation signatures in the enhancer segment, and the rules of transcription factor binding can, and do evolve within and around the enhancers. Such dynamic arrangements break the notion of modularity across evolutionary time: enhancer identity may be ultra-conserved, vanished, split, or duplicated with various consequences on neighboring genes. Locally, in some limited piece of evolutionary time, the enhancers may be modular, but globally such modularity may break.
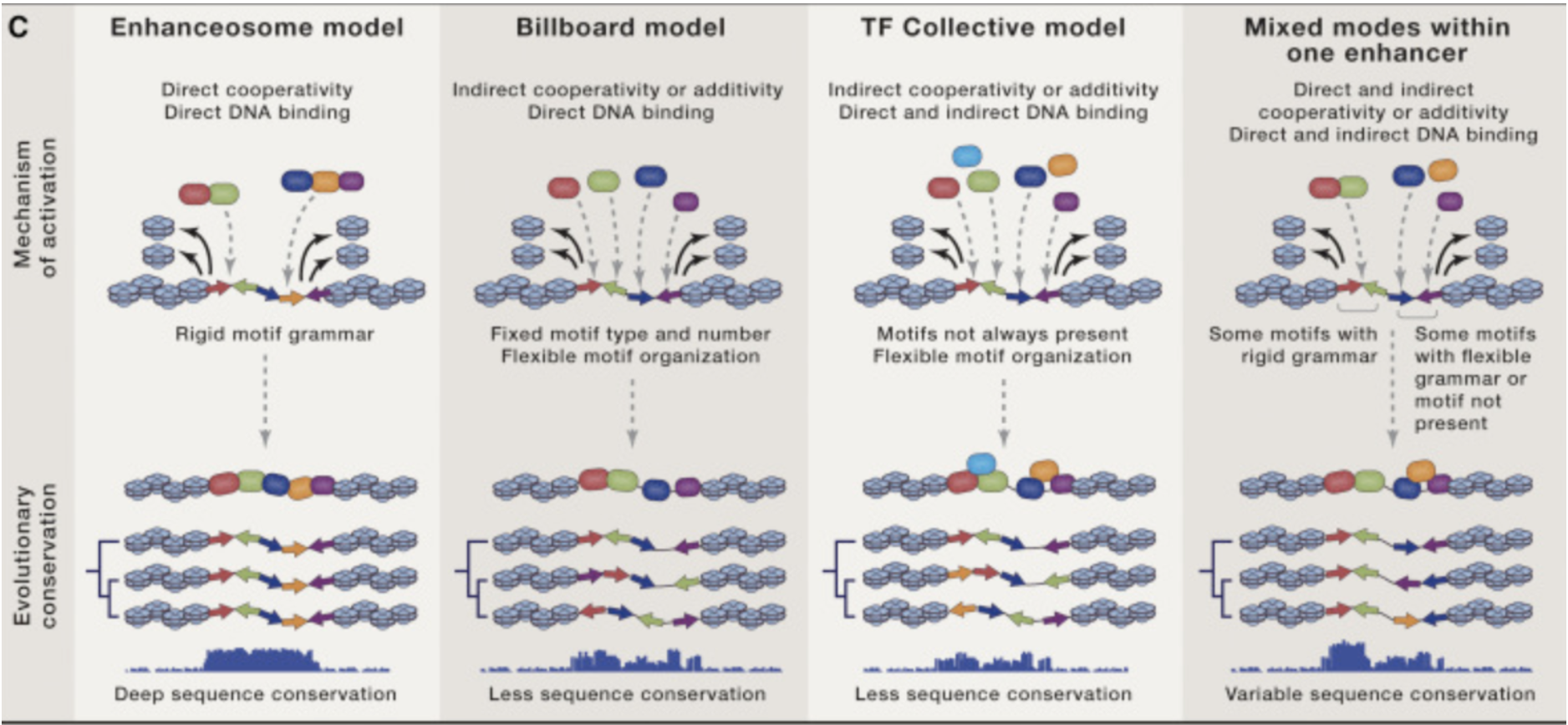 Different modes of cooperativity of transcription factor binding to activate an enhancer is reflected in a way by its conservation signature across species. These models are not set in stone as they may change from one mode to the next or disappear altogether depending on selection pressures. From: Long et al.
Different modes of cooperativity of transcription factor binding to activate an enhancer is reflected in a way by its conservation signature across species. These models are not set in stone as they may change from one mode to the next or disappear altogether depending on selection pressures. From: Long et al.
Causal multiplicity: polygenic models of gene-disease associations
We tend to think of machines as fixable entities. Even without knowing a machine’s blueprint, we might assume that the parts of the machine are specific to each function and we can thus reverse engineer how they work and how to fix it if it’s broken. In a way, we expect “causal transparency”: there should be a clear mechanism with a defined effect where we could potentially intervene. This assumption breaks down in many biological systems. Take for example gene-disease associations, where the goal is to find which genes are linked to which diseases, with the eventual objective to understand and possibly cure these conditions by targeting those genes or whatever they interact with. The classical approach to this problem is through genome-wide association studies (GWAS). In GWAS a large population containing individuals afflicted with a particular disease is genetically screened and then an association of each genetic variant screened with the disease is probed. At the beginning, the hope was that GWAS would nail down a handful of genes underlying a given condition, and while there were some successes, most diseases were associated either with more variants than expected or with regions of the genome that were hard to interpret. Eventually, it was recognized that most common diseases and traits were likely modulated by many many genes. Subsequently, various such polygenic models have been set forth including different flavors of omnigenic models where most genes are associated with any given trait with varying strengths of association. This is not to say that ventures associating genetic variation with disease are hopeless: indeed, the targets of successful drugs are enriched for genes that have been implicated genetically in disease, but rather that a great proportion of gene-disease causality has eluded us. Generally, for any given disease there are no single culprits and the underlying mechanisms are not a single path in a causal graph.
The machine metaphor in software
Design patterns of modularity, functional encapsulation, and re-use are part of the mantra of software engineering, and many software abstractions such as the object-oriented paradigm have leveraged machine metaphors to help practitioners write code with these properties. The very foundation of computer science is based on the Turing machine: an abstract tool described in very mechanistic terms as a tape reader and writer. The recent wave of tools for training machine learning models for computer vision, speech recognition, and natural language tasks has in some sense upended these notions so far as to be heralded as “Software 2.0”. Machine learning models depart from the neat modular and encapsulated approach to traditional software engineering where explicit instructions are given to the machine by casting problems as continuous optimization tasks. Instead of designing parts of the program as you would parts of a machine – as encapsulated components with a given function wired together in a specific way to produce a desired output – machine learning models are functions with parameters that are tweaked to maximize some optimization objective (such as the accuracy of translating speech to text). Even the task of designing the structure of a machine learning model (its parameters and the way they are connected) is sometimes relegated to another optimizer. Generally useful machine learning architectures, like attention mechanisms and convolutional layers, are proposed as abstractions that induce behaviors and biases in the model that might help it optimize better and faster. Nevertheless, in the end it is the optimizer that chooses the parameters for an instance of a machine learning model. The result is a somewhat opaque software artifact without a blueprint of what part does exactly what. In the absence of explicit design plans, there are several tools to make the model more interpretable or to gain insights into how it works. In a bit of an ironic twist, some techniques used to probe machine learning models are similar to the ones used to probe biological systems: techniques in which one systematically perturbs or removes part of the system and observes the effect. Such “ablation experiments” have become de rigueur in the artificial intelligence community when introducing new machine learning architectures. In this and other ways, the software produced by machine learning deviates a lot from the machine metaphor principles, as deliberate designs of modularity, decomposability, and purposefulness are not baked into the instance of the software itself but into its general recipe (that is, the machine learning architecture). This is not to say that machine learning model instances are not modular, but rather the modularity is an emergent property rather than explicitly designed. For example, a machine learning model instance that has been tasked with modeling language can allocate a portion of itself to learn to recognize emotions as a by-product. Indeed, this property has been taken advantage to the extreme in natural language processing, where there is a tendency to create models that just learn to model the structure of a language itself and hoping that as a by-product they will learn information useful for other tasks. This approach to designing software recognizes that many times tasks in the real world are defined by empirical examples and exploration, rather than by a hidden logical design that is heavily implied in machine metaphors.
General failings of the machine metaphor
Although I’ve given some examples on where machine metaphors fail to capture the nuances of systems in the real world, there are more fundamental problems that become apparent upon closer examination.
Reverse engineered networks are leaky abstractions: networks (poorly) hide other networks themselves
A machine’s blueprint specifies how and which parts of a system are connected, making it easy to understand each part within the context.. When reverse-engineering a system, it may be thus tempting to find “the blueprint” of connections. For sufficiently complex systems and/or in cases where we can’t observe all the relevant variables, this is an ill-posed task. We might get notions of dependencies and correlations between parts that we can observe and probe, but it will be generally impossible to ascertain the exact mechanism. Any such edge that we reverse-engineer might contain a hidden network within itself. For example, we might be able to figure out that a certain enhancer affects the expression of a certain gene through a certain transcription factor. If we do this for all known transcription factors and all genes we get a grand network of what turns on what gene. But within each of these edges lies several hidden variables. Are other factors required for the interaction? How effective is it? Is it dependent on a particular biological context? Such hidden networks make our grand network look more like a sketch than an actual blueprint, diminishing its utility.
All circuits are networks but not all networks are circuits.
Circuits are common machine metaphors used to describe systems ranging from the abstract, like statistical models, to the concrete, like cellular metabolic pathways. The main trait that the circuit metaphor evokes is information flow: given a diagram of the circuit’s components and some power sources, resistances, and modulators scattered throughout, there is an expectation of being able to characterize the circuit if we just analyze how the current flows through it. Circuit tools allow us to simplify this analysis by focusing on specific parts of the circuit at a time while conveniently reducing the rest to “black boxes”. Such simplifications are even possible with circuits that were not explicitly designed but rather evolved as is demonstrated by Thompson. In his study, when evolving an FPGA circuit for the task of tone discrimination using a genetic algorithm, the resulting circuit was only partially connected and subsequent analysis revealed that only a subset of circuit components was required for functionality.
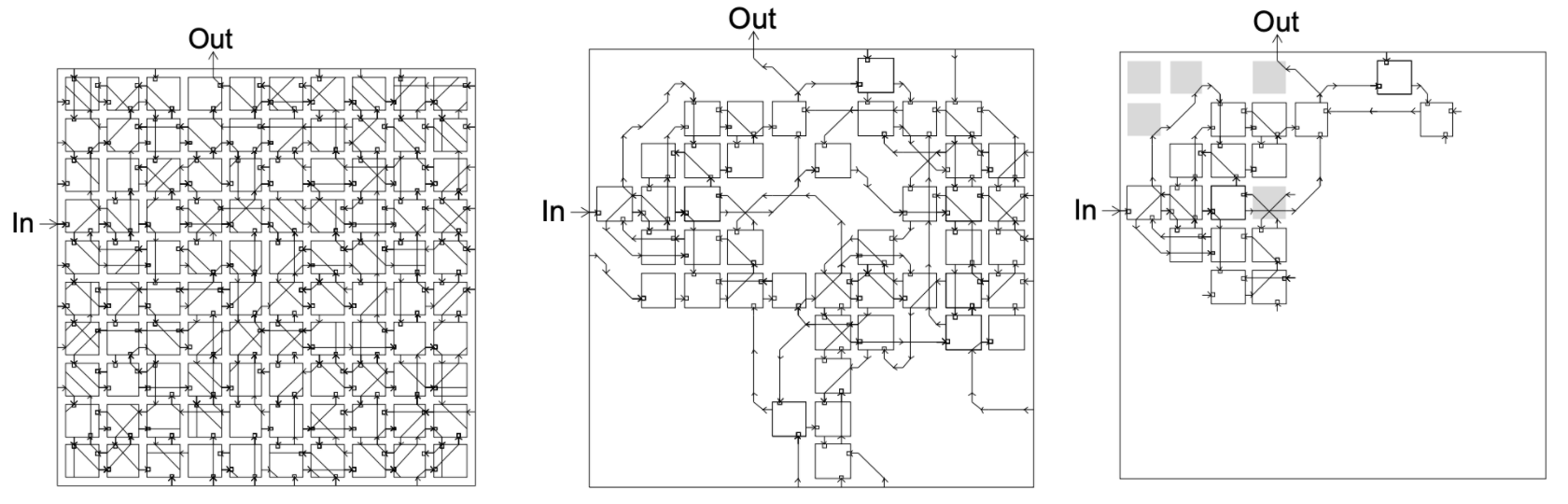 FPGA circuit evolved to solve the task of tone discrimination. Left: evolved circuit; Center: active parts of the circuit; Right: essential parts of the circuit with trivial modules grayed out. From Thompson
FPGA circuit evolved to solve the task of tone discrimination. Left: evolved circuit; Center: active parts of the circuit; Right: essential parts of the circuit with trivial modules grayed out. From Thompson
This “simplification through flow analysis” is a powerful circuit trait, but it doesn’t necessarily translate to other scenarios. Most crucially, it necessitates that only a handful of nodes in the network as outputs and that the output of the flow is connected to some predefined purpose (tone-discrimination in the previous example). Many other systems do not share these properties: metabolic and gene expression networks have a large “output surface” where many genes or metabolites are used downstream for several purposes. They are further subject to different evolutionary pressures that wax and wane over time. Perhaps as a result, the architecture of circuits and other technological networks tend to have different topological properties than networks that self-organize under multiple constraints, like in the case of biological and social networks. These technological networks tend to have more evidence for scale-free arrangements, where a fraction of nodes are responsible for the majority of connections.
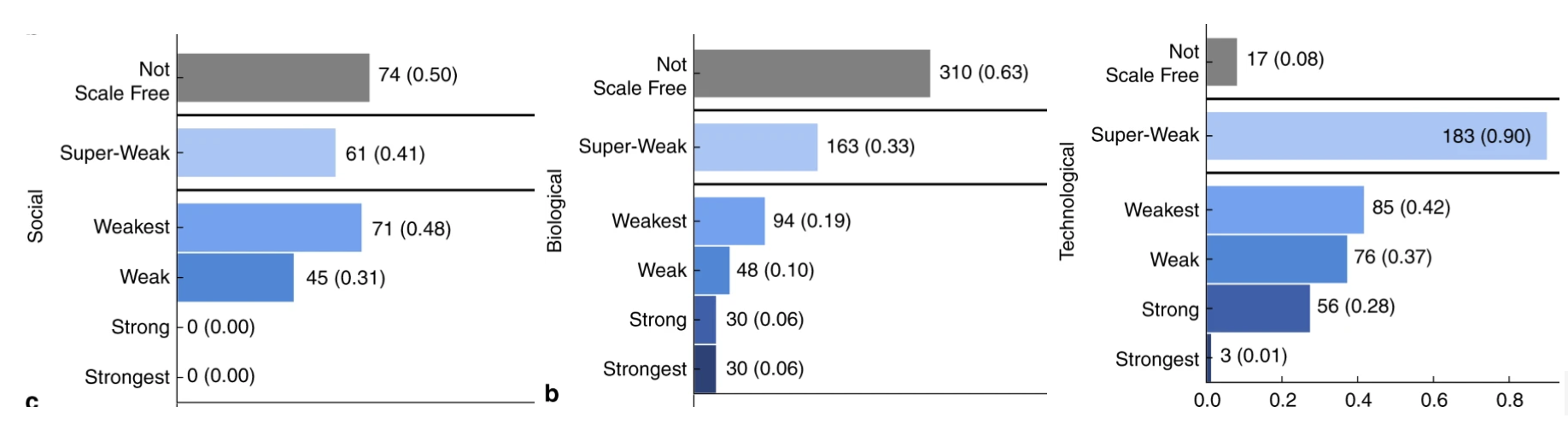 Number of networks exhibiting different evidence tiers for scale-free topologies in different network types. Scale-free networks are networks where the majority of connections can be found in a relatively few nodes. Taken from Broido and Clauset
Number of networks exhibiting different evidence tiers for scale-free topologies in different network types. Scale-free networks are networks where the majority of connections can be found in a relatively few nodes. Taken from Broido and Clauset
The limits of optimization
Machines tend to be built not only with a function in mind but also with specific constraints and thus their design is many times posed as a solution to some fixed optimization problem. Many systems do not emerge out of such single optimization processes. Biological systems find themselves under pressure from various sources in the environment and are more likely to emerge from multi-objective optimization processes rather than a single goal. Even then, environmental and genetic constraints ebb and flow in evolutionary time and can best be seen as temporary signals that nudge the system from one state to another. Such a paradigm can also be seen in modern machine learning models, which are products of multiple optimization processes themselves: instead of taking all training examples as a whole and finding the best parameters that model them, current optimization techniques typically nudge the system into one or another direction driven by a handful of samples at a time, perhaps randomly chosen from the training set. Limiting the influence of all samples this way seems to help rather than hurt the final result: the models tend to generalize better to other settings. In addition, producing better models does not only depend on the effectiveness of finding good solutions to the optimization problem, but also on acquiring more data to train on and altering the model’s architecture, further expanding the degrees of freedom one can take. In both biological and machine learning systems, where the optimization landscape is complex and the parameters are many, the optimization problem itself might be ill-posed, and is instead used as reference to guide the system so that it adapts to downstream environments.
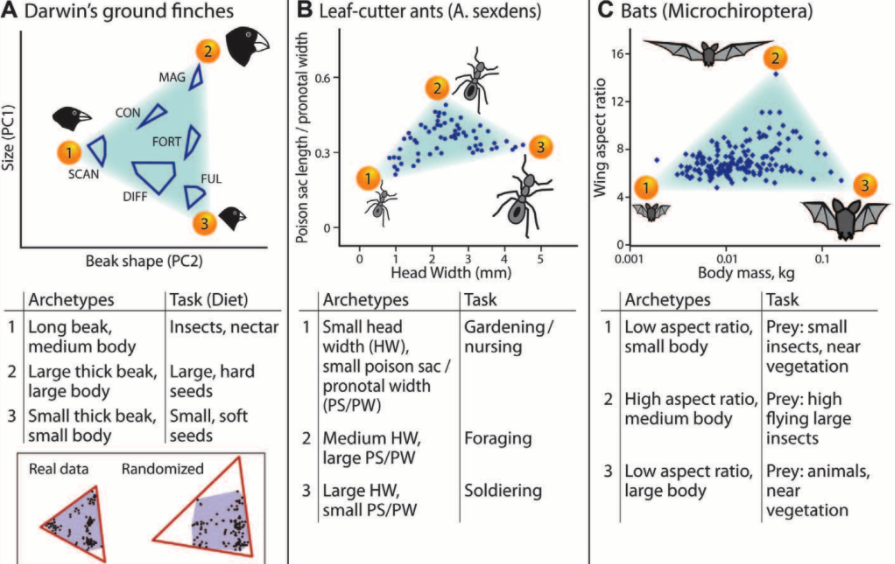 Biological systems produce phenotype spaces constrained by multiple optimization criteria. (from Sheftel et al.)
Biological systems produce phenotype spaces constrained by multiple optimization criteria. (from Sheftel et al.)
Whither to new metaphors?
This is where it gets interesting. Given that static and rigid machine metaphors have failed us when describing these dynamical systems with causal multiplicity in several fields, frameworks to understand them better have been set forth as alternative solutions. What’s striking is that regardless of the field, these solutions share some common threads that make them qualitatively the same. I will highlight three of these guiding threads below.
Systems as processes
In several of his works [raging against the machine metaphor](https://library.oapen.org/handle/20.500.12657/29752 and https://pubmed.ncbi.nlm.nih.gov/31173758/), Daniel J. Nicholson emphasizes the dynamical aspects of biological systems stating that they should not be thought as a collection of “things that change” but rather as “stability attained through change”. A gene is an identity of nucleotide sequence that achieves evolutionary stability given it’s viability to be expressed and the fitness it confers to the organism. Pretrained machine learning models are stable configurations in a giant parameter space that are useful for many downstream tasks. Languages themselves are stable rules of utterances and writing constrained by their social use. This is not in the least a novel way to think about systems. Vector fields, dynamical systems, and master equations are but a few frameworks that formalize this idea, and the whole area of complex systems makes it a central theme. What makes these frameworks more relevant is how ubiquitous their applicability has become. Thanks to a multitude of high-throughput methods developed in relatively recent years we are now able to follow the molecular states of thousands to millions of single cells through their development, the spiking trains of thousands of neurons. Additionally, our scaling computational infrastructure allows us to track the learning behaviors of enormous machine learning models, and the economic behavioral trajectories of entire societies. Across these frameworks, there are a few shared ideas that are important to highlight:
Systems are generally described through their variable components and the states those variables can take. Together, these form a “state space” and the system follows a trajectory inside that space. Each point in the state space has an associated direction, that we call velocity, and points where the system will go next. While the state spaces may be immense, the observed trajectories of the system fall in limited regions which are much lower in dimension. The discrepancy between all the possibilities of the system and the observed low dimension of the paths is due to the strength of the correlations between the components’ states: the more correlated they are, the more limited the space of the trajectory The jaggedness, twists, and turns – i.e. the geometry – of the observed trajectories is important for understanding key aspects of the system.
There’s surprising value in describing a process using some of the concepts in these frameworks, even if only done qualitatively. For example, let’s consider a system’s variable, state, and velocity. Additionally, let’s also inspect the geometry induced by the velocities further by looking at the acceleration and curvature, as conceptualized below.
Using these general concepts, the following table contrasts four very different systems: the expression of genes in developing cells, the coordinated spiking of a network of neurons, a molecule folding into its structure and the parameters of a machine learning model as it learns, much in the way Qiu et al. do in their work:
| System | State | Variables | Velocity | Acceleration | Curvature |
|---|---|---|---|---|---|
| Developing single cells | All genes in a cell | Vector of amount of expression of each gene | Direction of development | Developmental state commitment | Developmental state decision points |
| Spiking neurons | Neurons | Vector of number of spikes per neuron | Direction of neuron coordination | Coordination commitment to a learning hotspot | Coordination branching points |
| Molecular folding | Atom positions or bond angles | Vector of molecule’s configuration | Direction of force field | Force field acceleration | Quasi-stable states |
| Machine learning model | Model parameters | Model configuration | Loss function gradient | Sensitivity of parameters to samples (Magnitude of variance) | Sensitivity of parameters to samples (Model selection crossroads) |
Just filling the table above forces us to think about the system in detail. What does it mean for the system to evolve in its space, what are the interpretations of the speed and shape of the trajectories?
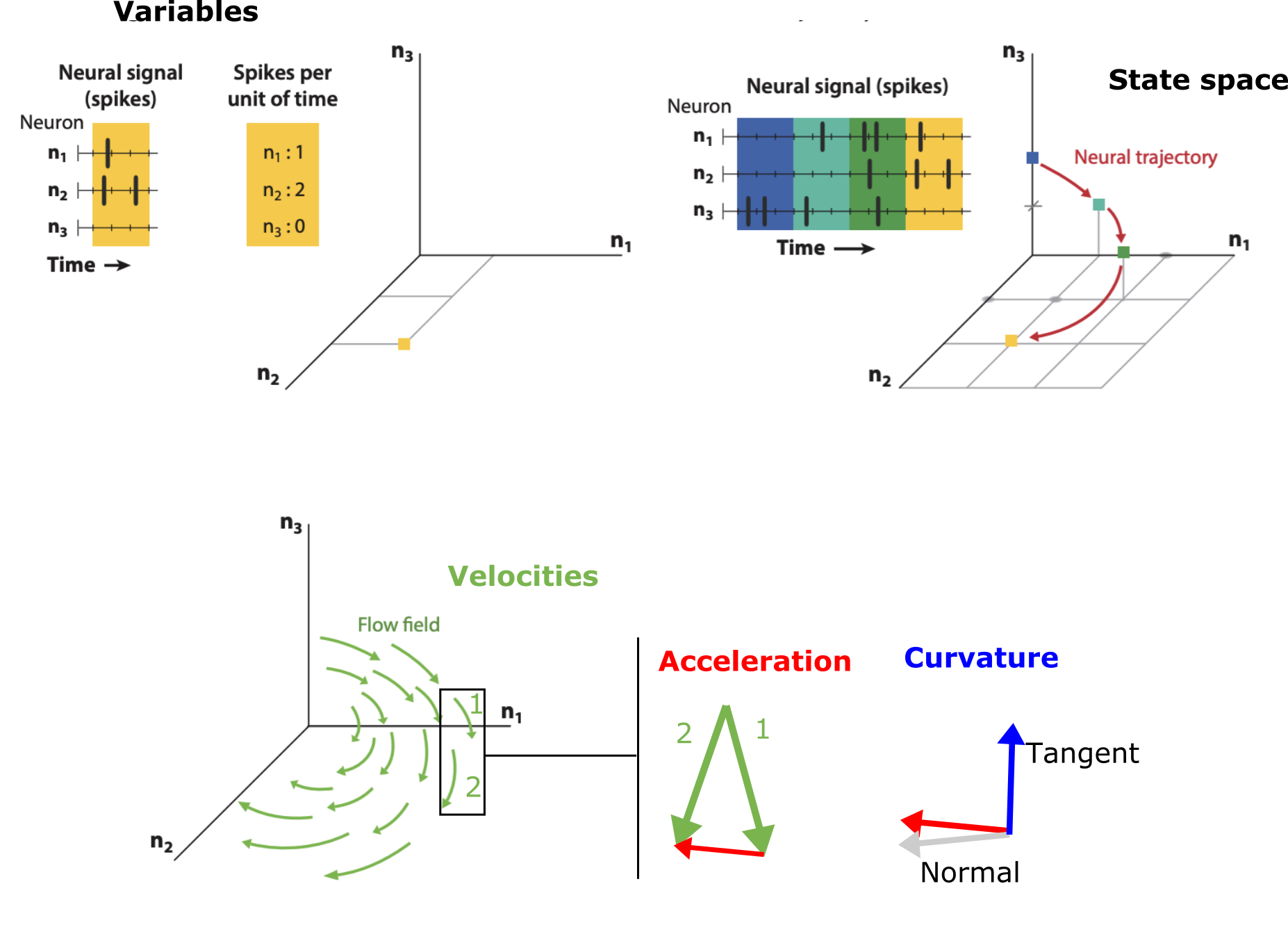 Broad, intuition overview of geometrical concepts in vector fields. Adapted from Vyas et al.
Broad, intuition overview of geometrical concepts in vector fields. Adapted from Vyas et al.
Causal motifs and causal model ensembles
Causality is somewhat of a scientific obsession. How do I know that the expression/existence of this gene causes this and other phenotypes? Can we predict what would happen if we give this medicine to an ailing patient? How can I build a robot that can understand and interrogate cause and effect?. For large and complex systems, the simple answer to the vast majority of causal questions is very likely to be: you can’t. Not with full certainty and limited observational data anyway. Many methods have been invented to try and extract causal relationships from observations, i.e. they try to get that “blueprint with arrows'' that tells us what to expect when you perturb a component of the system. These methods work as well as we can expect them to: we can get a notion of ‘strength’ of a causal relationship in a simple causal network model. There’s been quite a lot of work recently in inferring causality: both from observational data and from specifically designed experiments. While these efforts have bear great fruits in controlled settings, I don’t think they’ve succeeded in helping us understand and intervene in more complex and uncontrolled regimes. You see, the catch here is that you need to start with a causal model to begin with. What if your causal model is wrong? What if there is a better one? Enumerating all causal models of a system grows super exponentially with the number of variables in the system, you can’t possibly compare them all. At one point, there was a flurry of work to build clever methods that would sample relevant causal models. But while there is still some activity in that area, it has dwindled quite a bit. I think the main problem is that we don’t know yet how to think in terms of ensembles of causal models, to conceptualize a set of possible causal graphs. One option is taking the average of all causal connections and looking at the weights – “averaging out” the set of causal networks. The problem is that crucial information of each causal model is lost in this approach: e.g. colliding paths like $A \rightarrow C \leftarrow B$ are informative as a triplet, not edge by edge.
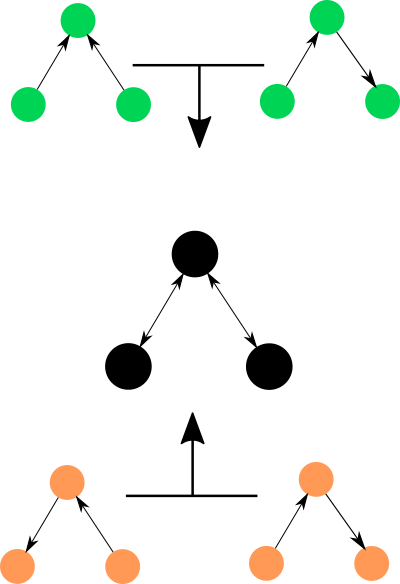 *Two very different sets of causal models can be averaged into the same single causal structure, making it difficult to interpret.*
*Two very different sets of causal models can be averaged into the same single causal structure, making it difficult to interpret.*
Instead, something like a bag of weighted network motifs might be a better way to conceptualize our uncertainty in this space. Highlighting and visualizing causal structure uncertainty is also an unsolved problem: it is not yet clear how to conceptualize a multitude of possible causal structures and how to leverage them to produce insights for performing actual interventions. In this front, the summed up magnitude of efforts to develop methods and frameworks to explore the causal universe is undeniable, but the direction is less clear.
System instances as experiments
Systems are never singletons. Even those we ourselves designed represent a snapshot of a creation process different from those that came before them and those that will come after. Nature is the most extreme of tinkerers as it tries billions upon billions things in parallel, all systems with slight modifications. In other words, each instance of a system is an experiment of sorts, each within different contexts. Phylogenetic trees have been used to visualize such differences in biology and chemistry, capturing flows of change. Could we do the same for any collection of evolving systems?
Putting it all together
What happens if we collate all of the characteristics highlighted previously? What kind of metaphors are created? Two paths come to mind:
- Complex systems are the metaphor: What if there are no really good metaphors to encompass all of these characteristics? What if the system itself has to become the metaphor? Metaphors seem to arise from widespread and practical human artifacts. Maps, atlases, clocks, machines, circuits, etc. Could “artificial intelligences” or “dynamical/biological systems” become metaphors themselves? Unfortunately, the names we have chosen for these things are very ambiguous without context, e.g. terms like “artificial intelligence” are highly problematic and already cause headaches in practitioner and non-practitioner communities alike. Just out of nomenclature these metaphors may fail to take hold.
- Something new: Try as I might, I can’t come up with a simple metaphor to communicate the complexity of the systems we face today. There might be something out there, but my guess is that it’s going to be something new: an amalgamation of the models we’ve tried so far.
Closing thoughts
Thanks to advances in several technologies for measuring and taking advantage of dynamical systems in different settings – molecules to organisms to artificial intelligences – there seems to be a conceptual momentum for a specific way to think about these disparate systems that departs from the limited machine metaphors of the past. Different as these systems may seem, they share certain structures, geometries, and uncertainties in the causal forces behind them that manifest in similar ways. Many mature frameworks for analyzing dynamical systems exist, so that part I think we have covered. Much less clear is how we are going to deal with the many times ambiguous causal structure underlying these systems, how to marry these causal uncertainties with system dynamics and how to use these concepts to analyze and design interventions. In a way, this reminds me of the time when fields like complex systems and systems biology were taking off. While incredibly useful tools, these fields in a way fell to their own hype….or maybe were waiting for the proper moment where a tsunami of measurements across all fields would vindicate them. Their time might finally have come.
Acknowledgements
Thanks to @io_chan for editing, cleanup suggestions and discussions!





